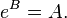geometria & trigonometria: FUNCIONES LOGARITMICAS

En matemáticas, el logaritmo de un número –en una base determinada– es el exponente al cual hay que elevar la base para obtener dicho número. Es la función matemática inversa de la función exponencial.
Logaritmación es la operación aritmética donde dando un número resultante y una base de potenciación, se tiene que hallar el exponente al que hay que elevar la base para conseguir el mencionado resultado. Así como la suma y multiplicación tienen como operaciones opuestas la resta y la división respectivamente, la logaritmación es la operación inversa a la exponenciación.

Logaritmos
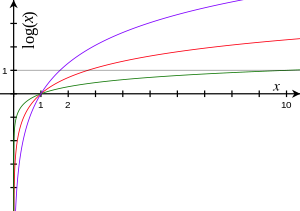Gráfica de Logaritmos
Definición	$\ln(x)=\int_1^x\frac{dt}{t}, x>0\,$
Tipo	Función real
Descubridor(es)	Nikolaus Mercator (1668)^[1]
Dominio	$]0,+\infty[$
Codominio	$]-\infty,+\infty[$
Imagen	$]-\infty,+\infty[$
Propiedades	Biyectiva Cóncava Estrictamente creciente
Cálculo infinitesimal
Derivada	$\frac{1}{x}$
Función inversa	$e^x\,$
Límites	$\lim_{x\to 0^+}\ln(x)=-\infty\,$ $\lim_{x\to+\infty}\ln(x)=+\infty\,$
Funciones relacionadas	Función exponencial
El rojo representa el logaritmo en base e. El verde corresponde a la base 10. El púrpura al de la base 1,7.

Concepto
Dado un número real (argumento x), la función logaritmo le asigna el exponente n (o potencia) a la que un número fijo (base b) se ha de elevar para obtener dicho argumento. Es la función inversa de la exponencial x = bⁿ. Esta función se escribe como: n = log_b x, lo que permite obtener n.

$\log_b x = n\Leftrightarrow\ x = b^n$

(esto se lee como: logaritmo en base "b" de "x" es igual a "n"; sí y solo si "b" elevado a la "n" da por resultado a "x")

La base b tiene que ser positiva y distinta de 1 $(b>0, b \ne 1)$ .
x tiene que ser un número positivo $(x > 0)$ .
n puede ser cualquier número real $(n\in\mathbb{R})$ .

Así, en la expresión 10² = 100, el logaritmo de 100 en base 10 es 2, y se escribe como log₁₀ 100 = 2.
Se denomina logaritmo neperiano (ln) o logaritmo natural al logaritmo en base e; fueron desarrollados por John Napier.
Los logaritmos de base 10, decimales, comunes o vulgares son aquellos en que la base es 10. Fueron inventados y desarrollados por Henry Briggs.
Para representar la operación de logaritmación se escribe la abreviatura Log y como subíndice la base y después el número resultante del que deseamos hallar el logaritmo. Ejemplo:

103 = 1000

luego

L o g 10 1000 = 3

.
Cuando se sobreentiende la base, se puede omitir. Para indicar logaritmos en base e se usa ln.

Historia

El método de cálculo mediante logaritmos fue propuesto por primera vez, públicamente, por John Napier (latinizado Neperus) en 1614, en su libro titulado Mirifici Logarithmorum Canonis Descriptio. Joost Bürgi, un matemático y relojero suizo al servicio del duque de Hesse-Kassel, concibió por primera vez los logaritmos, sin embargo, publicó su descubrimiento cuatro años después que Napier. La inicial resistencia a la utilización de logaritmos fue cambiada por Kepler, por el entusiasta apoyo de su publicación y la impecable y clara explicación de cómo funcionaban.
Este método contribuyó al avance de la ciencia, y especialmente de la astronomía, facilitando la resolución de cálculos muy complejos. Los logaritmos fueron utilizados habitualmente en geodesia, navegación marítima y otras ramas de la matemática aplicada, antes de la llegada de las calculadoras y computadoras. Además de la utilidad en el cálculo, los logaritmos también ocuparon un importante lugar en las matemáticas más avanzadas; el logaritmo natural presenta una solución para el problema de la cuadratura de un sector hiperbólico ideado por Gregoire de Saint-Vincent en 1647.
Napier no usó una base tal como ahora se entiende pero, sus logaritmos, como factor de escala, funcionaban de manera eficaz con base 1/e. Para los propósitos de interpolación y facilidad de cálculo, eran útiles para hallar la relación r en una serie geométrica tendente a 1. Napier escogió r = 1 - 10⁻⁷ = 0,999999 (Bürgi eligió r = 1 + 10⁻⁴ = 1,0001). Los logaritmos originales de Napier no tenían log 1 = 0, sino log 10⁷ = 0. Así, si N es un número y L es el logaritmo, Napier calcula: N = 10⁷(1 − 10⁻⁷)^L. Donde (1 − 10⁻⁷)^10⁷ es aproximadamente 1/e, haciendo L/10⁷ equivalente a log_1/e N/10⁷.
Inicialmente, Napier llamó "números artificiales" a los logaritmos y "números naturales" a los antilogaritmos. Más tarde, Napier usa la palabra logaritmo en el sentido de un número que indica una proporción: λόγος (logos) el sentido de proporción, y ἀριθμός (arithmos) significado número, y se define, literalmente, como «un número que indica una relación o proporción». Se refiere a la proposición que fue hecha por Napier en su "teorema fundamental", que establece que la diferencia de dos logaritmos determina la relación de los números a los cuales corresponden, de manera que una progresión aritmética de logaritmos corresponde a una progresión geométrica de números. El término antilogaritmo fue introducido a finales de siglo XVII y, aunque nunca se utilizó ampliamente en matemáticas, perduró en muchas tablas, hasta que cayó en desuso.

Definición analítica

Artículo principal: Logaritmo natural

En la imagen se puede ver la representación gráfica del logaritmo neperiano, como también la representación de las rectas tangentes a la función en x = e (T_e) y en x = 1 (T₁).

Podemos introducir la función logarítmica como una función analítica que es de hecho la función primitiva de otra función analítica bien conocida. Para definir de esa manera el logaritmo empezamos con algunas observaciones:

La derivada de la función $f(x) = x^n \,\!$ es $f^\prime(x) = nx^{n-1} \,\!$ . Al dividir ambos lados de la expresión entre "n" y observar el resultado, se puede afirmar que una primitiva de $x^m \,\!$ es ${x^{m+1}}/{m+1}\,$ (con $m = n - 1\,$ ).
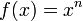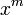Este cálculo obviamente no es válido cuando $m = - 1$ , porque no se puede dividir por cero. Por lo tanto, la función inversa $1/x\,$ es la única función "potencia" que no tiene una primitiva "potencia".
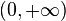Sin embargo, la función $1/x\,$ es continua sobre el rango $(0, + \infty)$ lo que implica que tiene forzosamente una primitiva en este intervalo, y también sobre $(- \infty, 0)$ .

A la función analítica cuya existencia se deduce de las observaciones anteriores la llamaremos función logaritmo, y la definiremos convencionalmente como:

$[\ln(x)]^\prime = \frac {1}{x}, \qquad \ln (1) = 0$

Propiedades de la función logarítmica

El dominio de la función 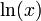$\ln(x)\,$ definida anteriormente es el conjunto de los números reales positivos.
$ln(x)$ es estrictamente creciente pues su derivada es estrictamente positiva.
Tiene límites infinitos en $0^+\,$ y en $+\infty$ .
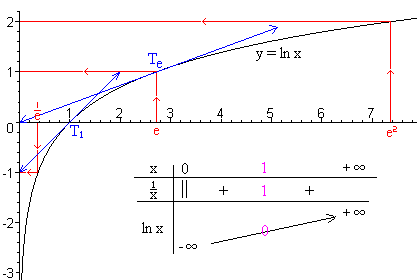
La tangente T_e que pasa por el punto de abscisa e de la curva, pasa también por el origen.
La tangente T₁ que pasa por el punto de abscisa 1 de la curva, tiene como ecuación: $y = x - 1$ .
La derivada de segundo orden es $\ln^{\prime\prime} (x) = {-1}/{x^2}\,$ , siempre negativa, por lo tanto la función es cóncava, hacia abajo, como la forma que tiene la letra "r", es decir que todas las tangentes pasan por encima de la curva. Es lo que se constata con T₁ y T_e.
La función logaritmo neperiano es la inversa de la función exponencial: $f(x) = e^x\;$ .

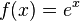Propiedades generales

Los números negativos no tienen logaritmo en el campo de los reales, ya que cualquiera sea u, es siempre $e u > 0$ (o $10 u > 0$ ) y en consecuencia no hay ningún valor de u que pueda satisfacer $e u = x$ cuando $x < 0$ , sin embargo, se pueden calcular logaritmos de números negativos recurriendo a la fórmula de Euler.
El logaritmo de su base es 1. Así $log b b = 1$ ya que $b 1 = b$ .
El logaritmo de 1 es cero (independientemente de la base). Así $log b 1 = 0$ ya que $b 0 = 1$ .
Si 0<A<1 entonces $log b A$ es un logaritmo negativo. Es lógico ya que el logaritmo de 1 es cero, entonces los menores que uno serán negativos por ser la función logarítmica estrictamente creciente.
Las potencias consecutivas de una base forman una progresión geométrica y la de los exponentes una progresión aritmética. Así las potencias de 2 son 1,2,4,8,16...etc y sus exponentes serán 0, 1, 2, 3, 4... etc ya que $20 = 1$ , $21 = 2$ , $22 = 4$ , $23 = 8$ , y $24 = 16$ etc. Luego $log 2 1 = 0$ , $log 2 2 = 1$ , $log 2 4 = 2$ , $log 2 8 = 3$ y $log 2 16 = 4$ etc.

Logaritmos decimales

Los logaritmos decimales tienen, en general, una parte entera y una parte fraccionaria.

Se denomina característica a la parte entera del logaritmo.
Se denomina mantisa a la parte fraccionaria (que puede ser cero).

La característica de un número comprendido entre 1 y 10 (excluido este) es cero. Es lógico ya que $L o g 10 1 = 0$ y $L o g 10 10 = 1$ entonces los números comprendidos entre 1 y otro menor que 10 serán decimales, con entero 0, que es su característica.
La característica de los números superiores o iguales a 10 será un número igual a la cantidad de cifras menos 1 del mencionado número. Así para 10, 20 o 30 su característica es 1; la de 150 es 2, etc.
La característica y mantisa de los logaritmos superiores a 1 será positiva.
La característica de los logaritmos entre 0 y 1 será negativa y su mantisa positiva.

Los logaritmos negativos se escriben en forma decimal con la característica subrayada seguido de la mantisa. Si un logaritmo negativo lo ponemos (–C,mantisa) indicaríamos que la mantisa es negativa; por eso se indica un línea horizontal encima de la característica, indicando que esta se tiene que restar y la mantisa sumar.

Identidades logarítmicas

Artículo principal: Identidades logarítmicas

Los logaritmos mantienen ciertas identidades aritméticas muy útiles a la hora de realizar cálculos:

El logaritmo de un producto es igual a la suma de los logaritmos de los factores.

$\!\, \log(a b) = \log(a) + \log(b)$

El logaritmo de un cociente es igual al logaritmo del numerador menos el logaritmo del denominador.

$\!\, \log(a / b) = \log(a) - \log(b)$

El logaritmo de una potencia es igual al producto entre el exponente y el logaritmo de la base de la potencia.

$\!\, \log(a ^ x) = x \log(a)$

El logaritmo de una raíz es igual al producto entre la inversa del índice y el logaritmo del radicando.

$\!\, \log(\sqrt[x]{y}) = \frac{\log(y)}{x}$

En realidad la tercera y cuarta identidad son equivalentes, sin más que hacer:

$\!\, \sqrt[x]{y} = y^\frac{1}{x}$

Cambio de base

Son comunes los logaritmos en base e (logaritmo neperiano), base 10 (logaritmo común), base 2 (logaritmo binario), o en base indefinida (logaritmo indefinido). La elección de un determinado número como base de los logaritmos no es crucial, ya que todos son proporcionales entre sí. Es útil la siguiente fórmula que define al logaritmo de x en base b (suponiendo que b, x, y k son números reales positivos y que tanto "b" como "k" son diferentes de 1):
$\log_b(x) = \frac {\log_k(x)}{\log_k(b)} \,\!$
en la que "k" es cualquier base válida. Si hacemos k=x, obtendremos:
$\log_b(x) = \frac {1}{\log_x(b)} \,\!$
En la práctica, se emplea el logaritmo decimal, que se indica como $\log(x)\,\!$ , en ciencias que hacen uso de las matemáticas, como la química en la medida de la acidez (denominada pH) y en física en magnitudes como la medida de la luminosidad (candela), del sonido(dB), de la energía de un terremoto (escala sismológica de Richter), etc. En informática se usa el logaritmo en base 2 la mayoría de veces.

Extensiones

Es posible extender el concepto de logaritmo más allá de los reales positivos.

Números reales

Para enteros b y x, el número

l o g b (x)

es irracional (no puede representarse como el cociente de dos enteros) si b o x tienen un factor primo que el otro no tiene.
El logaritmo natural de un número real positivo está bien definido y es un número real. Sin embargo, generalizar el logaritmo natural a números reales negativos sólo puede hacerse introduciendo números complejos.
Sin embargo, al igual que sucede el logaritmo de números complejos la elección de logaritmo de un número negativo no es única, aunque la elección hecha es la más frecuentemente usada para extender el logaritmo a números reales negativos.

Números complejos

El logaritmo natural de un número complejo z es otro número complejo b = ln(z) que sea solución de la ecuación:

(*) $z = e^b\;$

La ecuación anterior no tiene solución única. De hecho, tiene un número infinito de soluciones, aunque todas ellas son fáciles de encontrar. Dado un número complejo z escrito en forma polar, una solución posible de la ecuación (*) es b₀:

$b_0 = \ln \rho + i \theta \qquad \mbox{con}\ z = \rho e^{i\theta}$

Puede comprobarse que ésta no es la única solución, sino que para cualquier valor $k\in\mathbb{Z}$ resulta que el número complejo b_k, definido a continuación, también es solución:

$b_k = \ln \rho + i\theta + 2\pi ki \qquad \Rightarrow e^{b_k} = \rho e^{i\theta}\cdot e^{2\pi ki} = z$

De hecho cada valor particular de k define una superficie de Riemann.

Logaritmo en base imaginaria

Artículo principal: Logaritmo en base imaginaria

Un logaritmo en base imaginaria es un logaritmo que tiene como base i (la unidad imaginaria). Este tipo de logaritmos se puede resolver fácilmente con la fórmula:

$\log_i(z) = {{2 \ln(z) } \over i\pi} .\,$

Dónde z es cualquier número complejo excepto 0. Sin embargo, cabe señalar que la fórmula anterior sólo es una de las posibles soluciones ya que la ecuación:

$i^\lambda = z\,$

admite no sólo la solución dada anteriormente sino que cualquier x de la forma:

$\lambda = \frac{2}{i \pi}\ln(z) + 4k = \log_i(z) + 4k , \qquad k \in \mathbb{Z}$

también es solución.

Matrices

Artículo principal: Logaritmo de una matriz

Una matriz B es logaritmo de una matriz dada A si la exponenciación de B es A:

$e^B = A. \,$

A diferencia de la exponenciación de matrices, el logaritmo de una matriz real puede no estar definido siempre.
En el caso de una matriz diagonalizable es necesario que logaritmo esté definido para todos y cada uno de los autovalores o valores propios de la matriz. En ese caso el logaritmo de la matriz está definido y es una matriz real.
Si el logaritmo no está definido sobre el espectro o conjunto de autovalores, aún así es posible definir una matriz logaritmo (en forma similar a como se definen los logaritmos de números negativos o complejos), aunque no resulta única.
En el caso de una matriz no diagonalizable, este proceso es más complicado, ya que requiere encontrar primero su forma canónica de Jordan.